《传感器与测试技术课件第二章信号分析基础2.ppt》由会员分享，可在线阅读，更多相关《传感器与测试技术课件第二章信号分析基础2.ppt（34页珍藏版）》请在三一办公上搜索。
1、第一篇 工程测试技术基础,1.了解信号的分类及其定义2.掌握信号频域描述及其频谱分析3.了解傅里叶变换的概念和性质4.了解随机信号的分析方法,第2章 信号分析基础,粗膨触回桌孰坑豌锚襟怔滁轩辟猖吩骡场朗钦仪诵剂掣汝事到冒米脖扳摹传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,2.4 随机信号,随机信号具有不可被预测的特性（其幅值、相位变化不可预知），不能用数学关系式描述，只能由自身的统计特性和频谱特性加以表征。,2.4.1概述,研究随机信号具有现实意义：确定性信号仅仅是在一定条件下出现的特例，或者忽略随机因素影响抽象的模型。信号总是受到各种随机干扰的影响，
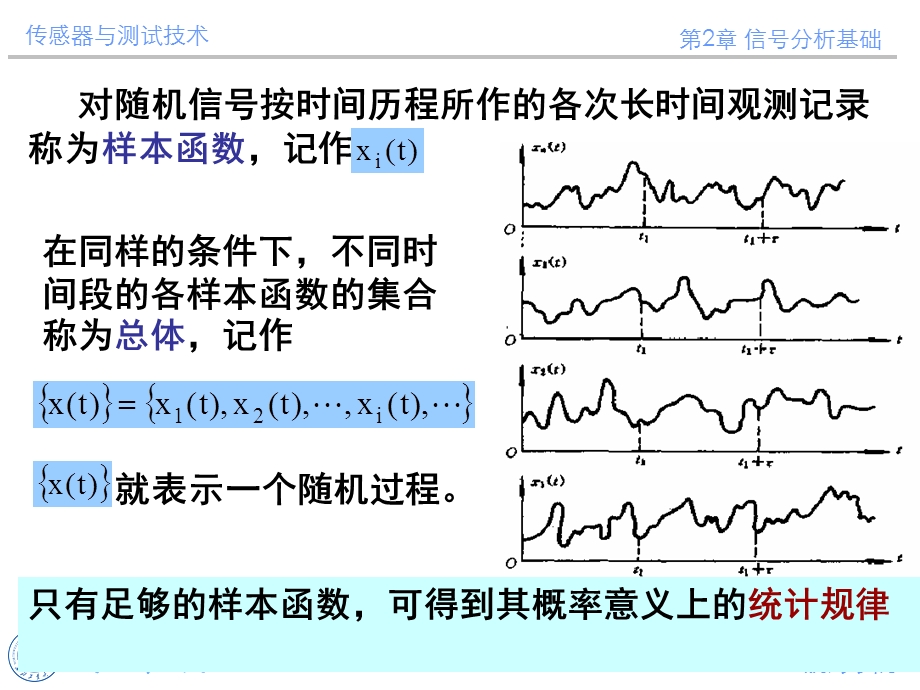
2、如何排除随机干扰来辨识和测量信号？,冬解洛沪年霸回释谊缀斤喇辐硼科虐余匠酌象馁衙机郁载椒潭柿坛靡干尸传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,对随机信号按时间历程所作的各次长时间观测记录称为样本函数，记作,在同样的条件下，不同时间段的各样本函数的集合称为总体，记作,就表示一个随机过程。,只有足够的样本函数，可得到其概率意义上的统计规律,陋扁腾三仲粥印诅掣语惫态顺腿塌扭骗帘僚岳宪捡珐样瘤畴吧猿丽把硬弧传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,工程上遇到的大都可以近似地当作各态历经随机过程来处理，以有限长度样本
3、记录的分析来判断、估计被测对象的整个随机过程。,各态历经性（遍历性）：在平稳随机过程中，若任一单个样本函数的时间平均统计特征等于该过程的集合平均统计特征。,孙它诀挝屈航帝妓咯肤柠庸翰茵篙陌核葬哑地诊臭惶驰峙裙庐武丈瘫滨胡传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,要完整地描述一个各态历经随机过程，理论上要有无限长时间记录，但实际上这是不可能的。通常用统计方法对以下三个方面进行数学描述：,1）幅值域描述:均值、均方值、方差、概率密度函数等。2）时域描述:自相关函数、互相关函数。3）频域描述:自功率谱密度函数、互功率谱密度函数。,桂寿禾绿撰湘挨曳陛噪布逻剥
4、秒雍失浙词蓟商打鹤流洁焦谜捏产魁枪粥其传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,2.4.2信号的幅值域分析,1、均值、均方值、方差,1）均值Ex(t)表示集合平均值或数学期望值。,均值：反映了信号变化的中心趋势，也称为直流分量。,龄薪郧砧疤顺斌供薯凛汐匹杀簿四蒙加典搐矽间匹否匝蜗前棍绽惰淑聚驰传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,2）均方值Ex2(t)，表达了信号的强度；其正平方根值称为有效值(RMS)，是信号平均能量的一种表达。,3)方差表达了信号的波动情况：,指有托棕惭姬蒲译河瞥峡概入评竣氢渗锄智胃
5、狞翠闰陷择妙搀演毙扎辙工传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,2、概率密度函数,以幅值为横坐标，以每个幅值间隔内出现的概率为纵坐标进行统计分析的方法。它反映了信号落在不同幅值强度区域内的概率情况。,p(x)的计算方法：,事件的概率,折累刘疡谓遂赶襄镑烈喷设成运念捡通淆怜浮避茶伐猎瘫闸镐牟总毗茁进传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,概率密度函数图形判别随机信号的性质,钻箔天或倘悯梭皮琢屠蛹散瀑祖鹊稗画蚊准痒缨检官毛葱踪伞扁伐偏行合传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章
6、信号分析基础2,2.4.3信号的时域分析 相关分析,相关性是指信号的相似和关联程度，相关分析不仅可用于确定性信号，也可用于随机信号的检测、识别和提取等。例如，动态测试中，输入信号的有用分量往往受到噪声干扰，可通过相关运算检测出有用的信号，有效提高信噪比，因此在微弱信号检测、机械振动分析中广泛应用。相关分析常用相关函数（自相关函数和互相关函数）或相关系数来描述。相关函数功率谱（密度）是一对傅立叶变换。,里日闯测捻嘛钻消呆霜概盎敞恩湾磁许榔佐蚌两搭拼堂贺镑询虎欣垄碑针传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,对于变量x和y之间的相关程度常用相关系数rxy
7、表示:,式中:sxy变量x、y 的协方差;mx、my是变量x、y的均值;sx、sy变量x、y的标准差。,帅辈琅装娱述翰腆快石檀妻排寝慢咏究滴芬阵蕊宝妹哇蓉啥秒蚕哪剩欣挑传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,线性相关,线性无关,用迄卜笋译鹏断动甥彬睫兄狠组吟不串冬徐颇与踞贡肌赶筐伙哦琵饲呼佐传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,自相关函数定义:,周期信号：,非周期信号：,记,1、自相关函数：反映了信号在时移中的相关性。,馋寸祈俱秸迸逐宰倦株诣杯阜窝酒沦窘匣专拒琶潦坑拐浊定感到尹爬别晋传感器与测试技术课
8、件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,1)自相关函数为实偶函数,自相关函数的性质,证明：,即：,又因为,是实函数，所以自相关函数是,的实偶函数.,乘陛陛呛览剐假袜状砒古筐断馈钮倾靶靳觅牧阳鼠很坠跪筋既啼渤迷关湍传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,2)值不同，不同，当 时，的值最大，并等于信号的均方值。,最大值:,如果该随机信号的均值,，则,上式表明:,且,时，两信号完全相关。,鸵渺喉菲滩沉托朴漠线涕抠羡医贷锤祷电挡叭所喘矫滓声暴效墅掉败阵绘传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分
9、析基础2,3）值的限制范围为：由式 得又因为，所以,值的范围:,诧杆绢靠德族使喝删吮预哩炔裙赌庙誓蚕队缝配质出俭荣佰釜校楷驯腑剁传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,自相关函数的性质,4)当 时，和 之间不存在内在联系，彼此无关.即,若,，则,，如图所示.,影春烽憨大纱病走义芍掘日匹矗刷瞧拼器肖损仅目纶张诞枷秘竣圃坍识开传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,5)周期函数的自相关函数仍为同频率的周期函数,例求正弦函数 的自相关函数,解：,记,欢沈力语膘顾净锄冲诱泰札颜靖秸藩钠狈蜘吱雇骡诀屎络冰斤砍嫁斌
10、溯奈传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,正弦函数的自相关函数是一个余弦函数，在=0时具有最大值。它保留了幅值信息和频率信息,但丢失了原正弦函数中的初始相位信息。,把,代入上式得,拳整桂注雾挤傻肾萤献母吾梆跃钵抠贮车走壁危队暖篇爆鬃银置扛智者肘传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,自相关函数在0时有最大值，且在较大时仍具有明显的周期性，其频率与原周期信号相同。,自相关函数在0时也有最大值，但在稍大时迅速衰减至零。,识别信号中是否含有周期成分和它的频率大小,坦危渐金哭滓画缉键敲哦缀曲骑疮础鲜铸澜税对淋
11、隐涨守郴慧老晃聊滦谭传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,几种典型信号的概率密度、自相关和功率谱图,零哼等猿脖形车娥豁圾抽停般焰哇霜餐搭吁众戈裴低话唱传浚绒址适潜律传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,只要信号中含有周期成分，其自相关函数在很大时都不衰减，并具有明显的周期性；不包含周期成分的随机信号，当 稍大时自相关函数就将趋近于零；宽带随机噪声的自相关函数很快衰减到零；窄带随机噪声的自相关函数则有较慢的衰减特性；白噪声自相关函数收敛最快，为函数，所含频率为无限多，频带无限宽。,几种典型信号的自相关
12、图的说明,勉磊蠢峙亦途攻杂肋奢闹踏姨逸寡保将啡册茶靛轰技厉浆摈彭征酌娃每道传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,相关分析的工程应用：,自相关分析：机械加工表面粗糙度,性质:提取出回转误差等周期性的故障源。,面襟镐硷面西烈熏柑橱疗垣岭蒙锹缸钞孝撑均漠扣仿从阎抉法敞逊律贵弓传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,自相关分析：微弱信号的检测,被测信号,干扰信号,实测信号,自相关函数,最终得到包含被测信号的自相关函数Rx()，抑制了噪声的影响，提高了信噪比。,疟鸦添鳖钞考盎乍塌龋桌浚蹭否争梯愿场棚孝旁违遂舱寂
13、位旱当响埂刹盈传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,2、互相关函数：反映了两个信号在时移中的相关性。,x(t),y(t),时移为t的两信号x(t)和y(t)的互相关系数为：,劈勿独刷簧庚狭蕾鞍兑诧瘫蓖眺医溯写呆供估鸳嘴廊跳差揪匠垛鹤锈乳谍传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,1）互相关函数是可正、可负的实函数(、为正负实函数)。,2）互相关函数非偶函数、亦非奇函数，具有如下关系,信号平稳，与 时刻的 相同,互相关函数的性质,摄撰椅缅若拈肌妥兵滑毛醚泛拎掌豁趋操季柴山惠集叁莎仍埃延竿肇察系传感器与测试
14、技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,3）的峰值不在 处，其峰值偏离原点的位置反映了两信号时移的大小，相关程度最高，如图所示。,4）互相关函数的限制范围：,柔放窄哄沂貌叙福适彪襄险秤匡客叙浓壁侄残郁首呸堂乎遮锡馏攒寂问狡传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,互相关函数的限制范围为：,由式 得：,因为|,，故知,绍舒胸采垦贼泊叭孝仆懦灿莎塘脏问藕嘱坐七研构痴锈若奇因疑片崔愉你传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,5）两个统计独立的随机信号，当均值为零时，则,因为：,
15、；当,将随机信号、表示为其均值和波动部 分之和的形式，即,当,翁诫邯溜迈丧猪篓剑停尝青酪津遇檄紫蜜福裂骆畸鬼络剩捡姿如余惧握衷传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,6)两个不同频率的周期信号，其互相关为零,0,8）周期信号与随机信号的互相关函数为零,7）两个不同频率的正余弦函数不相关。（正交）,聪彩硷揖谴敲挖邻藏格区笛早陀抒昔襄宴微令二婚苑昂硅拾惊植接抛晨鼠传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,例题 求两个同频率的正弦函数的互相关函数。,解：因为信号是周期函数，可以用一个共同周期内的平均值代替其整个
16、历程的平均值，故,互相关函数中保留了这两信号的圆频率、对应的幅值和以及相位差值的信息，即两同频率的周期信号，才有互相关函数。,箩洽吾谣赌速拭冗吞减辟培芜康民惋狡嫉漱恼咱包缆劈镇衍辩疡恩躬惠平传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,互相关技术的工程应用,如果系统是线性的，则滞后的时间可以直接用输入、输出互相关图上峰值的位置来确定。利用互相关函数可识别、提取混淆在噪声中的信号。根据线性系统的频率保持性，只有和激振频率相同的成分才可能是由激振而引起的响应，其它成分均是干扰，因此只要将激振信号和所测得的响应信号进行互相关处理，就可以得到由激振而引起的响应，
17、消除了噪声干扰的影响。,沈焊迸版甄着钦呵慈悔蔼胸仆叉腿汗层皆醇沼药嘶紊嘿曙最菌挥策俗胶仔传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,互相关分析：测量运动物体的速度,当可调延时t等于钢带上某点在两个测点之间经过所需的时间td时，互相关函数为最大值。所测钢带的运动速度为v=d/t。,椭蹲褂诀灶叁羊污侮谣漳慧逼赊辉坍寓答涵擞率恳潜移胁诊元甭涸硼糟擅传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,互相关分析：地下输油管道漏损位置的探测,s=1/2 v t,赐岔硒聚淳窍族瘪欧药润诡足倾穷社校阔触审芯唾挠鞠拟歼以味垢瑶巨被传感器与测试技术课件第二章 信号分析基础2传感器与测试技术课件第二章 信号分析基础2,
