竞赛课件18：电容器.ppt

《竞赛课件18：电容器.ppt》由会员分享，可在线阅读，更多相关《竞赛课件18：电容器.ppt（32页珍藏版）》请在三一办公上搜索。

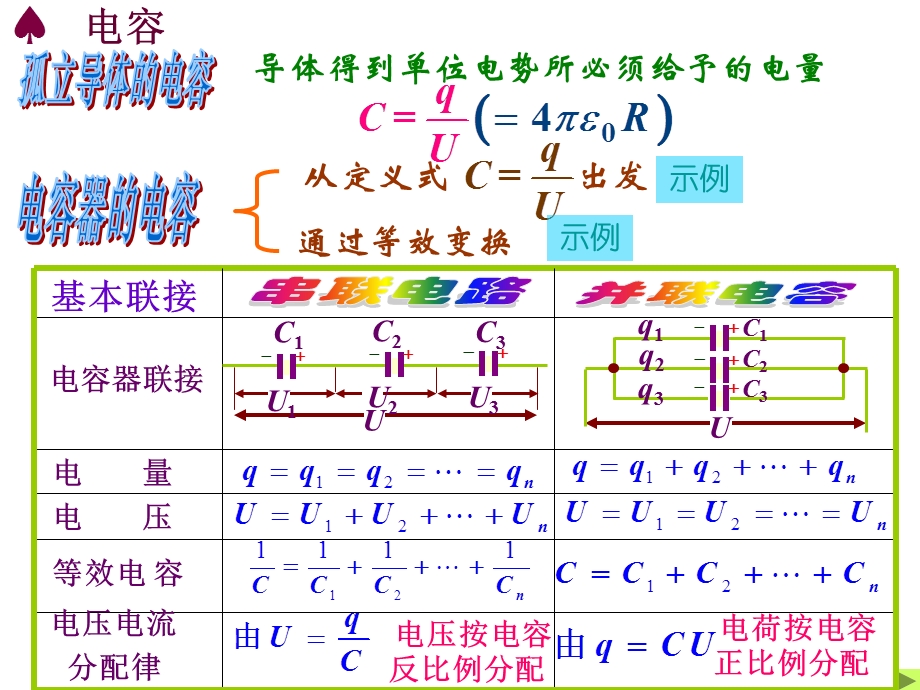
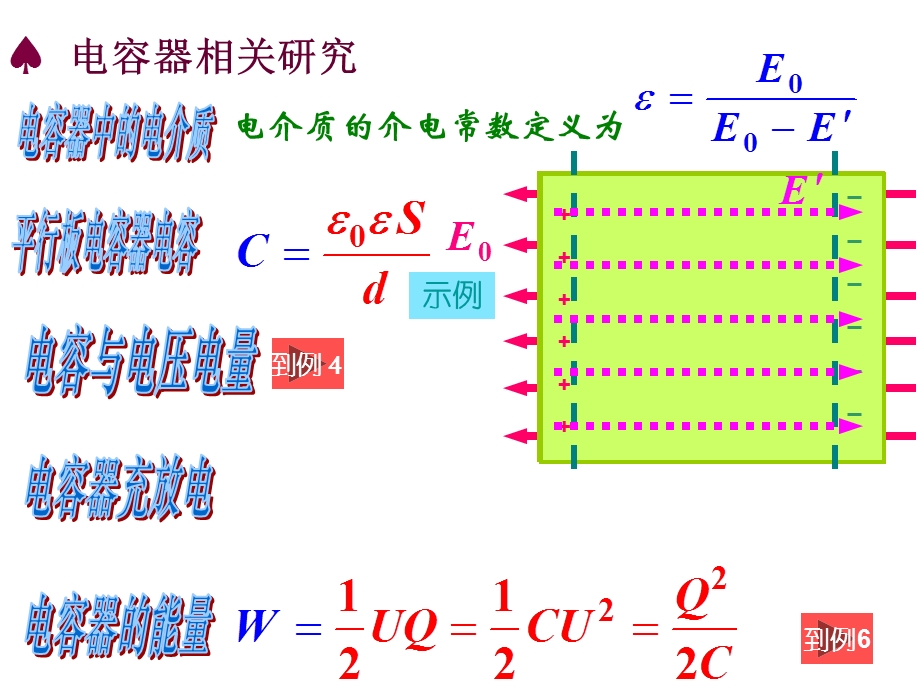
1、电容器,电容,孤立导体的电容,导体得到单位电势所必须给予的电量,电容器的电容,从定义式,出发,通过等效变换,电容器联接,电 量,电 压,等效电 容,电压电流 分配律,电压按电容反比例分配,电荷按电容正比例分配,示例,示例,电容器相关研究,电容器中的电介质,电介质的介电常数定义为,平行板电容器电容,电容与电压电量,电容器充放电,电容器的能量,到例,到例6,示例,由高斯定理,无限大均匀带电平面的电场由,两面积S、间距d平行板电容器当带电荷量Q时，板间电场由电场叠加原理可得为,平行板电容器,两板间电势差,球形电容器,由高斯定理,在距球心ri处场强,在距球心ri处,其上场强视作恒定,则元电势差为,电容

2、器两极间电势差为,两个半径均为R的导体球相互接触形成一孤立导体，试求此孤立导体的电容,解题方向:若能确定系统电势为U时的电量Q,可由定义求得C,考虑其中1球,电势为U时,电量,引入同样的第2球,1球将电势叠加,为维持U,对称地,为维持球2电势U,亦设置像电荷予以抵消,为抵消像电荷引起的电势,再设置下一级像电荷,专题18-例2,半径分别为a和b的两个球形导体，相距很远地放置，分别带有电荷qa、qb，现用一金属导线连接，试求连接后每球上的电荷量及系统的电容.,小试身手题6,解题方向:系统总电量守恒，只要确定导线连接后系统的电势,可由定义求得C,设连接后两球各带电,由电荷守恒有,由等势且相距很远,解

3、得,返回,解题方向:不平行电容器等效为无穷多个板间距离不等的平行板电容器并联!,用微元法,若无穷均分b,若无穷均分C,等式两边取n次方极限得,如图，两块长与宽均为a与b的导体平板在制成平行板电容器时稍有偏斜，使两板间距一端为d，另一端为（dh），且h d，试求该空气电容器的电容,专题18-例1,如图所示，由五个电容器组成的电路，其中C14F，C26F，C10F，求AB间的总电容,小试身手题1,设在A、B两端加一电压U，并设UMUN,M(N)处连接三块极板总电量为,则有,解得,于是有,五电容连接后的等效电容为,五电容连接直观电路如图,如图是一个无限的电容网络，每个电容均为C，求A、B两点间的总电

4、容,小试身手题4,设n个网格的电容为Cn,则有,整理得,该无穷网络等效电容为,n,返回,如图，一平行板电容器，充以三种介电常数分别为1、2和3的均匀介质，板的面积为S，板间距离为2d试求电容器的电容,专题18-例3,等效于C1与串联的C2、C3 并联:,在极板面积为S，相距为d的平行板电容器内充满三种不同的介质，如图所示如果改用同一种介质充满板间而电容与之前相同，这种介质的介电常数应是多少？如果在3和1、2之间插有极薄的导体薄片，问的结果应是多少？,小试身手题2,a,b,c,d,将电容器划分为如图所示a、b、c、d四部分,所求等效电容为a与b串联、c与d串联后两部分并联而成，由C可得,插入导体

5、薄片,所求等效电容为1与2并联与3串联，由C可得,球形电容器由半径为r的导体球和与它同心的球壳构成，球壳内半径为R，其间一半充满介电常数为的均匀介质，如图所示，求电容.,小试身手题3,球形电容器的电容,本题电容器等效于介电常数为和的两个半球电容器并联，每个半球电容各为,该球形电容器的等效电容为,R,r,如图所示为共轴的两导体圆柱面组成的电容器长l、半径分别为r和R两圆筒间充满介电常数为的电介质求此电容器的电容,小试身手题5,圆柱面电容器,设圆柱面电容器电容为C，它由n个电容为nC的元圆柱面电容串联而成，元圆柱面电容器可视为平行板电容器，第i个元电容为,ri,ri-1,解题方向:介质变化的电容器

6、等效为无穷多个介质不同的平行板电容器串联!,用微元法,无穷均分C,等式两边取n次方极限得,x,0,D,ri-1,ri,1,2,返回,1,2,3,4,+q1,-q2,+q2,-q1,解题方向:利用电容对两板间的电压及极板上的电量的制约,四块同样的金属板，每板面积为S，各板带电量分别为q1、-q1、q2、-q2各板彼此相距为d，平行放置如图，d比板的线尺寸小得多，当板1、板4的外面用导线连接，求板2与板3之间的电势差,专题18-例4,如图所示，两块金属平板平行放置，相距D=1 cm，一板上电荷面密度1=3C/m2，另一板上电荷面密度2=6C/m2，在两板之间平行地放置一块厚d=5 mm的石蜡板，石

7、蜡的介电常数=2求两金属板之间的电压,专题18-例5,如果在每个金属板上附加面密度为-4.5C/m2的电荷，电容器的带电就成为“标准状况”了两板带等量异种电荷:,附加电荷在板间引起的电场互相抵消，并不影响原来的板间电场，也不会改变电容器的电势,等效电容为:,电容为C的平行板电容器的一个极板上有电量q，而另一个极板上有电量+4q，求电容器两极板间的电势差,小试身手题,如果在每个金属板上附加-2.5q的电荷，电容器的带电就成为两板带等量异种电荷1.5q 的“标准状况”：,三个电容分别为C1、C 2、C 3的未带电的电容器，如图方式相连，再接到点A、B、D上这三点电势分别为A、UB、D则公共点O的电

8、势是多大？,小试身手题9,解题方向:考虑电容器电容、电压与电量之间的关系,设三个电容带电量分别为,如图所示的两块无限大金属平板A、B均接地，现在两板之间放入点电荷q，使它距A板r，距B板R求A、B两板上的感应电荷电量各如何？,小试身手题10,解题方向:与设想将q均匀细分n份，均匀分布在距板r处的平面M后等效,M,这是两个电容并联!,两电容器电容之比,并联电容总电量,每个电容带电量,设三块板上电量依次为q1、q2、q3，由电荷守恒：,1、2两板间的电场是三板上电荷引起电场的叠加：,3、2两板间的电场也是三板上电荷引起电场的叠加：,三块相同的平行金属板，面积为S，彼此分别相距d1和d2起初板1上带

9、有电量Q，而板2和板3不带电然后将板、分别接在电池正、负极上，电池提供的电压为U若板1、3用导线连接如图，求1、2、3各板所带电量？,小试身手题11,返回,S4断开，S1、S2、S3接通的条件下，三电容器并联在电源上，电路情况如图所示：,C1,C2,C3,S4,S2,S3,R,S1,每个电容器电量为,断开 S1、S2、S3接通S4的条件下，三电容器串联在电源上，电路情况如图所示：,由电荷守恒：,q1,-q2,q2,-q1,q3,-q3,由电势关系：,A,B,原来电容以C0表示，由电容器电容公式,板间距离为0.9d时,情况1中电容器两板间电压恒为U,情况2中电容器板上电量恒为C0U,A板引起的场

10、强是电容器板间场强的一半！,B板上的电量,比较两式得,在光滑绝缘水平面上，平行板电容器的极板A固定，极板B用绝缘弹簧固定在侧壁上，如图所示，若将开关S闭合，极板B开始平行地向极板A移动，到达新的平衡位置时两极板间距离减少了d1=10%如果开关闭合极短时间后就立刻断开（此间设极板B未及从原位置移动），求此后极板B到达新的平衡位置时两极板间距离减少的百分比d2,专题18-例7,解题方向:把介质拉出的过程,视为外力克服电场力做功消耗电场能的过程!,设将介质沿b拉出两板边缘x,外力大小为F,由功能关系：,两块平行金属板，面积都是ab，相距为d，其间充满介电常数为的均匀介质，把两块板接到电压为U的电池两

11、极上现在把板间介质沿平行于b边慢慢抽出一段，如图，略去边缘效应及摩擦，求电场把介质拉回去的力,专题18-例8,U,相互插入前：,故两电容器总电能,按第1种方式 插入:,+Q,-Q,+2Q,-2Q,按第2种方式 插入:,-Q,+Q,-Q,+Q,极板相同的两个平行板空气电容器充以同样电量第一个电容器两极板间的距离是第二个电容器的两倍如果将第二个电容器插在第一个电容器的两极板间，并使所有极板都互相平行，问系统的静电能如何改变？,小试身手题12,电容器带电时，上极板所受电场力矩与质量为m的砝码重力矩平衡，即,静电天平的原理如图所示，一空气平行板电容器两极板的面积都是S，相距为x，下板固定，上板接到天平

12、的一头，当电容器不带电时，天平正好平衡然后把电压U加到电容器的两极上，则天平的另一头须加上质量为m的砝码，才能达到平衡求所加的电压U,小试身手题13,充电完毕时各块板上电量均为,C,C,C,接入两电阻,电荷重新分布!,三电容成并联,故每个电容带电量为,释放的热量即减少的电场能,为,每个电阻放热,三只电容均为C 的电容器，互相串联后接到电源上，电源电动势为当电容器完全充电后跟电源断开，然后接入两只电阻均为R的电阻器，如图所示试问每只电阻上释放的热量有多少？当中间一只电容器的电压减小到电源电动势的1/10的瞬间，流过电阻R的电流i1和i2各为多大？,小试身手题14,双刀双掷开关,a,b,C2输出电

13、压U1=U/2,C2充电至q1=CU/2,双刀双掷开关,C1充电至电压U、电量CU,双刀双掷开关,C2充电至q2=5CU/4,C2输出电压U22=5U/4,双刀双掷开关,C2充电至q3=13CU/8,C2输出电压U23=13U/8,由此类推,如图所示，两个电容均为C的电容器C1和C2，一个双刀双掷开关S，一个可提供恒定电压U的蓄电池E将它们适当联接并操作开关，以使这个电路的输出端得到比U高的电压，试求出这个最高输出电压？,小试身手题15,(a)两块边长为15 cm的正方形平板，相距为5 cm，组成一个空气平行板电容器8.8510-12 F/m试求该电容器的电容电容器平板被竖直固定在绝缘支撑物上

14、（b）涂有导电漆的球形木髓小球被长为10 cm的一段丝线悬挂，丝线上端固定于A板上，如图所示，木髓小球开始时和A板接触它的质量m0.1 g，半径r0.3 cm，求木髓小球的电容 平板电容器的B板接地，A板与电势为60000V范德格喇夫起电机做瞬时接触，然后平板电容器再次绝缘这时可观察到木髓小球离开A板运动到B板，然后再返回到A板，往复几次以后，木髓小球处于平衡位置，并且悬挂丝线与A板夹角为(a)解释木髓小球为什么会这样运动并求出它最后的平衡位置；(b)计算两平行板之间最终电势差；(c)试求木髓小球在静止前来回摆动的次数k；(d)作一草图，表示两板电势差与小球在两板间来回次数的函数关系UABf(

15、k),小试身手题16,解答,(a)由平行板电容器公式得空气平行板电容器电容：,(b)由孤立导体球电容器公式得木髓球电容器电容：,(a)球带电后被A板静电推斥，与B板接触时放电而后受重力作用摆回A板充电，再被推到B板放电，如此往复k次，使板间电压减小、场强减小，直至小球所受电场力与重力及丝线张力平衡而静止在将要接触B板但未放电的位置，则丝线与A板夹角为,(b)由于球平衡，有,(c)初时A板与球电势均为U0=60000 V，球推开后A的电势变成U1，板上电量CU1，球上电量C0 U0，由电荷守恒：,由此类推,(d),读题,要使总电容最大，采用并联形式为好，故首先设计将小板联在一个电势点，大板联在一个电势点，这就相当于51个电容为,并联!,增大正对面积是增大电容的又一途径:,设隔板向右发生一小位移x，两侧气体对隔板的压力：,隔板上电荷受两侧电场静电力合力：,隔板所受合力：,简谐运动,一直向右（左）靠到盒右（左）侧,静止在新位置,