《抛物线及其标准.ppt》由会员分享，可在线阅读，更多相关《抛物线及其标准.ppt（61页珍藏版）》请在三一办公上搜索。
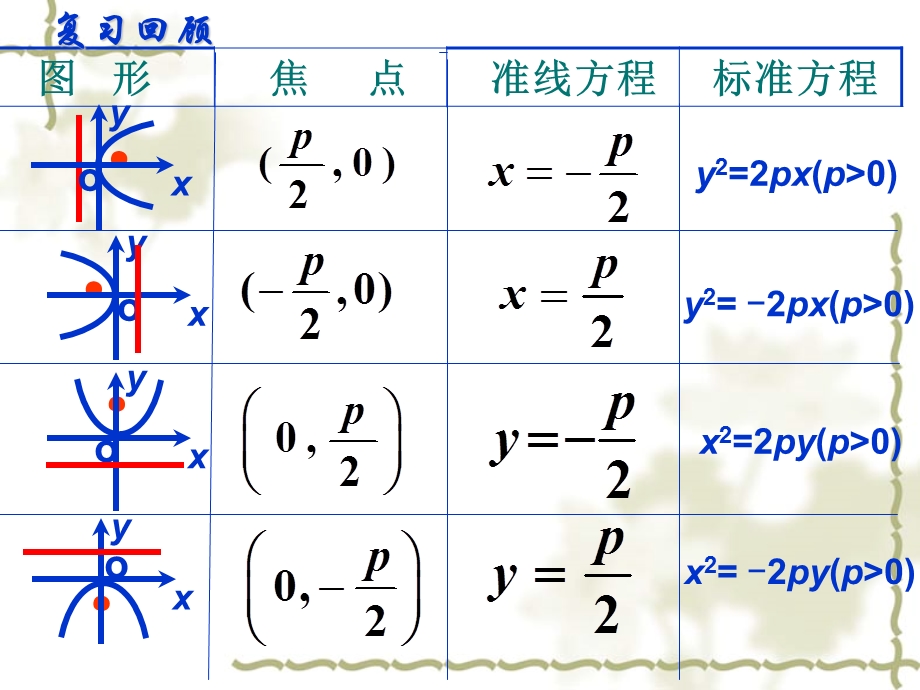
1、,2.4.1 抛物线及其标准方程,y2=-2px(p0),x2=2py(p0),x2=-2py(p0),y2=2px(p0),复习回顾,抛物线的四种标准方程对比,2.如何根据抛物线的标准方程来判断抛物线的焦点位置及开口方向？,焦点在一次项字母对应的坐标轴上.,一次项系数的符号决定了抛物线的开口方向.,1.抛物线的四种标准方程形式上有什么共同特点?,左边都是平方项，右边都是一次项.,题型一（由方程求有关量）,感悟：求抛物线的焦点坐标和准线方程要注意两点:1.先化为标准方程 2.判断焦点的位置,即：准确“定型”,练习：填空（顶点在原点，焦点在坐标轴上）,开口向右,开口向左,开口向上,开口向下,1.
2、焦点为F（-2，0），则抛物线的标准方程为_.2.准线方程是y=-2，则抛物线的标准方程为_.3.焦点到准线的距离是4,则抛物线的标准方程为_ _.,y2=-8x,x2=8y,y2=8x、x2=8y,（1）,（2）,题型二（由有关量求标准方程）,感悟：1.“定型”“定量”2.如果焦点位置或者开口方向不定则要注意分类讨论.,4.标准方程中p前面的正负号决定抛物线的开口方向,1.抛物线的定义:,2.抛物线的标准方程有四种不同的形式:每一对焦点和准线对应一种形式.,3.p的几何意义是:,焦 点 到 准 线 的 距 离,例1（1）已知抛物线的标准方程是y2=6x，求它的焦点坐标和准线方程；,（2）已知
3、抛物线的方程是y=6x2，求它的焦点坐标和准线方程；,（3）已知抛物线的焦点坐标是F（0，-2），求它的标准方程。,1 12,练习1：,1、根据下列条件，写出抛物线的标准方程：,（1）焦点是F（3，0）；,（2）准线方程 是x=；,（3）焦点到准线的距离是2。,y2=12x,y2=x,y2=4x、y2=-4x、x2=4y 或 x2=-4y,课堂练习,2、求下列抛物线的焦点坐标和准线方程：(1)y2=20 x(2)x2=y(3)2y2+5x=0(4)x2+8y=0,（5，0）,x=-5,（0，-2）,y=2,思考:M是抛物线y2=2px（p0）上一点，若点 M 的横坐标为x0，则点M到焦点的距离
4、是,这就是抛物线的焦半径公式!,3、(1)抛物线y2=2px（p0）上一点M到焦点的距离是a，则点M到准线的距离是_，点M 的横坐标为_,P67练习3(1),a,3、(2)抛物线y2=12x上与焦点的距离等于9的点的坐标为_,P67练习3(2),3,-3,2.若抛物线y2=8x上一点M到原点的距离等于点M到准线的距离，则点M的坐标是_.,变式练习:已知抛物线的焦点在 x 轴上，抛物线上的点M(-3,m)到焦点的距离等于5，求抛物线的标准方程.,数形结合,用定义转化条件。,5.求过点A（-3，2）的抛物线的标准方程.,感悟：1.待定系数法 2.数形结合 3.分类讨论,题型三（由有关量求标准方程）
5、,4.求焦点在直线3x+4y-12=0上的抛物线的标准方程.,题型三（由有关量求标准方程）,标准方程对应的抛物线焦点在坐标轴上.,分析:,例2 点M与点F(4,0)的距离比它到直线l：x+5=0的距离小 1，求点M的轨迹方程.,解：如图,设点M的坐标为(x,y),依题意可知点M与点F的距离等于它到直线x+4=0的距离，根据抛物线的定义，点M的轨迹是以F（4,0）为焦点的抛物线.,焦点在x轴的正半轴上，点M的轨迹方程为：y2=16x,l,x,O,y,F,题型四 抛物线的应用,例3:一辆卡车高3 m,宽1.6 m,欲通过断面为抛物线形的隧道,如下图所示,已知拱口AB宽恰好是拱高CD的4倍,若拱宽为
6、a m,求能使卡车通过的a的最小整数值.,分析:要求拱宽a的最小值,需建立适当的坐标系,写出抛物线方程,然后利用方程求解.,题型一 利用抛物线的定义求方程例1:若动圆M与圆C:(x-2)2+y2=1外切,又与直线x+1=0相切,则动圆圆心的轨迹方程是()A.y2=8x B.y2=-8xC.y2=4x D.y2=-4x,答案:A,解析:如图所示,设动圆圆心为M(x,y),半径为R,由题设可知定圆圆心为C(2,0),半径r=1.两圆外切,|MC|=R+1.又动圆M与已知直线x+1=0相切,圆心M到直线x+1=0的距离d=R,|MC|=d+1.即动点M到定点C(2,0)的距离等于它到定直线x+2=0
7、的距离.由抛物线的定义可知点M的轨迹为以C为焦点,x+2=0为准线的抛物线,其方程为y2=8x.故正确答案为A.,变式训练1:动点P到点(3,0)的距离比它到直线x=-2的距离大1,则动点P的轨迹是()A.椭圆 B.双曲线C.双曲线一支 D.抛物线解析:将直线x=-2向左平移一个单位,由已知可得动点P到点(3,0)的距离等于到直线x=-3的距离.,答案:D,2.抛物线y2=8x的准线方程是()A.x=-2 B.x=-4C.y=-2 D.y=-4答案:A,解析:y2=8x=24x,p=4,准线方程为,答案:B,解析:x2=ay的准线方程为,a=-8.,答案:C,答案:B,6.在平面直角坐标系xO
8、y中,已知抛物线关于x轴对称,顶点在原点,且过点P(2,4),则该抛物线的方程为_.,y2=8x,解析:设抛物线方程为y2=ax,又抛物线过点P(2,4),则16=2a,a=8,y2=8x.,7.(2008上海,6)若直线ax-y+1=0经过抛物线y2=4x的焦点,则实数a=_.,-1,解析:由y2=4x得焦点F(1,0),代入直线方程得a+1=0.a=-1.,11.(2010福建卷)以抛物线y2=4x的焦点为圆心且过坐标原点的圆的方程为()A.x2+y2+2x=0 B.x2+y2+x=0C.x2+y2-x=0 D.x2+y2-2x=0,解析:抛物线y2=4x的焦点坐标为(1,0),圆心坐标为
9、(1,0),半径r=1,圆的方程为(x-1)2+y2=1,即x2+y2-2x=0.答案:D,题型二 求抛物线的标准方程例2:求适合下列条件的抛物线的标准方程.分析:首先需确定使用哪种标准方程形式,若无法确定,则应讨论,然后由条件求p的值.,例2:求适合下列条件的抛物线的标准方程.(1)过点(-3,2);,(2)令x=0,由方程x-2y-4=0得y=-2,当抛物线的焦点为F(0,-2)时,设抛物线方程为x2=-2py(p0),则由=2得p=4,所求抛物线方程为x2=-8y.令y=0,由方程x-2y-4=0得x=4,当抛物线的焦点为F(4,0)时,设抛物线方程为y2=2px(p0),则由=4得p=
10、8,所求抛物线方程为y2=16x.综上,所求抛物线方程为x2=-8y或y2=16x.,例2:求适合下列条件的抛物线的标准方程.(2)焦点在直线x-2y-4=0上;,(3)焦点到准线的距离为 p=所求抛物线方程为:y2=5x或y2=-5x或x2=5y或x2=-5y.规律技巧:(1)抛物线的标准方程有四种形状,主要看其焦点的位置和开口方向.(2)不知道焦点的具体位置时,标准方程有两种一般形式:y2=mx(m0)或x2=ny(n0).,例2:求适合下列条件的抛物线的标准方程.(3)顶点在原点,以坐标轴为对称轴,焦点到准线的距离为,变式训练2:分别求满足下列条件的抛物线的标准方程.(1)过点(3,-4
11、);,解:(1)点(3,-4)在第四象限,设抛物线标准方程为y2=2px(p0)或x2=-2p1y(p10).把点(3,-4)的坐标分别代入y2=2px和x2=-2p1y,得(-4)2=2p53,32=-2p15(-4),(2)令x=0得y=-5,令y=0得x=-15.抛物线的焦点为(0,-5)或(-15,0).故所求的抛物线的标准方程为x2=-20y或y2=-60 x.,变式训练2:分别求满足下列条件的抛物线的标准方程.(2)焦点在直线x+3y+15=0上.,1.到定点(3,5)与定直线2x+3y-21=0的距离相等的点的轨迹是()A.圆 B.抛物线C.线段 D.直线,解析:因为定点(3,5
12、)在直线上,所以点的轨迹是直线.答案:D,方法：利用平移,3.动点P到点A(0,2)的距离比到直线l:y=-4的距离小2，则动点P的轨迹方程为_,x2=8y,1.抓住标准方程的特点,注意与焦点位置,开口方向的对应关系;2.抛物线的定义反映了抛物线的本质，灵活应用定义往往可以化繁为简、化难为易，且思路清晰，解法简捷，巧妙解法常常来源于对定义的恰当运用.,题型三 与抛物线有关的最值问题例3:已知抛物线x2=4y,点P是抛物线上的动点,点A的坐标为(12,6).求点P到点A的距离与点P到x轴的距离之和的最小值.,提示：利用准线,分析:由定义知,抛物线上的点P到焦点F的距离等于点P到准线的距离d,求|
13、PA|与点P到x轴的距离之和的最小值,转化成求|PA|+d-的最小值.,解:如下图,易判断知点A在抛物线外侧,设P(x,y),则P到x轴的距离即y值,设P到准线y=-1的距离为d,则y=d-1.,故|PA|+y=|PA|+d-1,由抛物线定义知|PF|=d.于是|PA|+d-1=|PA|+|PF|-1.由图可知,当APF三点共线时,|PA|+|PF|取最小值为13.故所求距离之和的最小值为|FA|-1=12.,规律技巧:定义是解决问题的基础和灵魂,要善于思考定义和应用定义,本题如果设P点坐标为(x,y),利用两点间距离公式求解,无法得到答案.由抛物线定义可知,|PF|等于P点到准线的距离,当P
14、AF三点共线时,|PA|+|PF|的距离最小,这体现了数学中的转化思想.,变式训练3:(2008辽宁高考)已知点P是抛物线y2=2x上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为(),解析:由抛物线的定义可知,抛物线上的点到准线的距离等于到焦点的距离.由图可知,P点,(0,2)点和抛物线的焦点(0.5,0)三点共线时距离之和最小.,答案:A,1.已知定点A(3,2)和抛物线y2=2x,F是抛物线焦点，试在抛物线上求一点P,使 PA与PF的 距离之和最小，并求出这个最小值.,提示：利用点到直线距离定义及二次函数最值,提示：利用准线,规律技巧:这是抛物线的应用问题.
15、解题时,可画出示意图,帮助理解题意,转化为数学问题,作出解答.,变式训练4:某河上有座抛物线形拱桥,当水面距拱顶5 m时,水面宽8 m,一木船宽4 m,高2 m,载货后木船露在水面上的部分高为 m,问水面上涨到与拱顶相距多少时,木船开始不能通航?,答:水面上涨到与抛物线拱顶相距2 m时,船开始不能通航.,8.(2009海南宁夏卷)已知抛物线C的顶点为坐标原点,焦点在x轴上,直线y=x与抛物线C交于A,B两点,若P(2,2)为AB的中点,则抛物线C的方程为_.,y2=4x,解析:设抛物线方程为y2=ax(a0),由方程组得交点坐标为A(0,0),B(a,a),而点P(2,2)为AB的中点,从而a=4.故所求抛物线方程为y2=4x.,9.已知抛物线的焦点在y轴上,抛物线上一点M(m,-3)到焦点的距离为5,求m的值,抛物线标准方程和准线方程.,10.探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60 cm,灯深为40 cm,求抛物线的标准方程和焦点位置.,解:如下图在探照灯的轴截面所在平面内建立直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合,x轴垂直于灯口直径.,设抛物线的标准方程是y2=2px(p0).由已知条件可得点A的坐标是(40,30),代入方程,得302=2p40,即所求的抛物线标准方程为,焦点,答案:B,
